Binary Search Tree in java

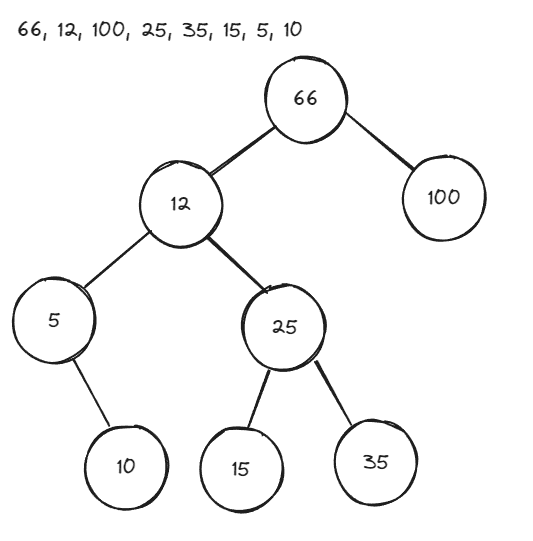
First we add these numbers into a Binary Search Tree (BST): 66, 12, 100, 25, 35, 15, 5, 10
Here we consider different orders and see how the BST will be created.

Lets implement BST in java.

public class TreeNode {
   private int data;
   private TreeNode left;
   private TreeNode right;
   public TreeNode(int data) {
       this.data = data;
   }
   public void insert(int inputData) {
       // we do not add duplicates, so avoid duplicates
       if (data == inputData) {
           return;
       }
       if (inputData < data) {
           if (left == null) {
               left = new TreeNode(inputData);
           } else {
               left.insert(inputData);
           }
       } else {
           if (right == null) {
               right = new TreeNode(inputData);
           } else {
               right.insert(inputData);
           }
       }
   }
   public void traverseInOrder() {
       if (left != null) {
           left.traverseInOrder();
       }
       System.out.print(data + ", ");
       if (right != null) {
           right.traverseInOrder();
       }
   }
}

public class Tree {
  private TreeNode root;
  public void insert(int data) {
      if (root == null) {
          root = new TreeNode(data);
      } else {
          root.insert(data);
      }
  }
  public void traverseInOrder() {
      if (root != null) {
          root.traverseInOrder();
      }
  }
}

public class Main {
  public static void main(String[] args) {
      Tree bst = new Tree();
      // Note: Here we try to input same numbers but in different sequence to see how BST is build each time.
//        int[] inputArray = {66, 12, 100, 25, 35, 15, 5, 10}; // bst-1.png
//        int[] inputArray = {5, 10, 15, 66, 12, 100, 25, 35}; // bst-2.png
      int[] inputArray = {25, 12, 66, 10, 15, 35, 100, 5}; // bst-3.png
      for (int i=0; i< inputArray.length; i++) {
          bst.insert(inputArray[i]);
      }
      bst.traverseInOrder();
  }
}

Console output

    5, 10, 12, 15, 25, 35, 66, 100, 
    Process finished with exit code 0